Phương Pháp Quy Nạp Toán Học (Mới 2022 + Bài Tập)

– Nội dung của phương pháp quy nạp toán học (gồm hai bước và bắt buộc theo trình tự nhất định).

Bạn đang xem: Phương pháp quy nạp toán học

– Nắm rõ các bước của phương pháp quy nạp.

2. Kỹ năng:

– Sử dụng phương pháp quy nạp thành thạo.

– Biết cách lựa chọn và sử dụng phương pháp quy nạp hiệu quả.

3. Thái độ:

– Rèn luyện tư duy logic, hệ thống, linh hoạt. Biết quy lạ về quen.

– Cẩn thận chính xác trong lập luận quy nạp. Rèn luyện tư duy toán học vô hạn.

II. Phương pháp – phương tiện:

1. Phương pháp dạy học:

– Vấn đáp gợi mở.

– Nêu vấn đề, giải quyết vấn đề.

2. Phương tiện – chuẩn bị của thầy và trò:

– Giáo viên: chuẩn bị câu hỏi gợi mở.

– Học sinh: đọc trước bài, ôn tập kiến thức về mệnh đề ở lớp 10.

 

5 trang | Chia sẻ: lephuong6688 | Lượt xem: 6631 | Lượt tải: 9

Bạn đang xem nội dung tài liệu Giáo án môn Toán khối 11 – Phương pháp quy nạp toán học, để tải tài liệu về máy bạn click vào nút DOWNLOAD ở trên
Giáo án: PHƯƠNG PHÁP QUY NẠP TOÁN HỌCThời lượng: 2 tiếtĐối tượng học sinh: lớp 11 (Trung bình)Tiết theo PPCT: 37 – 38I. Mục tiêu bài dạy:1. Kiến thức: Học sinh nắm được:- Nội dung của phương pháp quy nạp toán học (gồm hai bước và bắt buộc theo trình tự nhất định).- Nắm rõ các bước của phương pháp quy nạp.2. Kỹ năng:- Sử dụng phương pháp quy nạp thành thạo.- Biết cách lựa chọn và sử dụng phương pháp quy nạp hiệu quả.3. Thái độ:- Rèn luyện tư duy logic, hệ thống, linh hoạt. Biết quy lạ về quen.- Cẩn thận chính xác trong lập luận quy nạp. Rèn luyện tư duy toán học vô hạn.II. Phương pháp – phương tiện:1. Phương pháp dạy học:- Vấn đáp gợi mở.- Nêu vấn đề, giải quyết vấn đề.2. Phương tiện – chuẩn bị của thầy và trò:- Giáo viên: chuẩn bị câu hỏi gợi mở.- Học sinh: đọc trước bài, ôn tập kiến thức về mệnh đề ở lớp 10.III. Phân phối thời lượng:Tiết 1: Phần lý thuyết Tiết 2: Phần bài tập
IV. Tiến trình bài dạy:Giáo viên
Học sinh
Bổ sung
Hoạt động 1: Ổn định lớp- Sỹ số lớp.- Kiểm tra tình hình chuẩn bị bài của học sinh.Hoạt động 2: Dẫn dắt khái niệm1. Mệnh đề là gì? Mệnh đề chứa biến là gì?2. Cho hai mệnh đề chứa biến “” và “” với .a. Với thì và đúng hay sai?b. Với thì và đúng hay sai?
Giáo viên phát vấn:- Với thì và đúng hay sai?- Chúng ta có thể kiểm tra hết tất cả các giá trị của n không? Vì sao? Một số mệnh đề liên quan đến số tự nhiên là đúng với mọi n mà chúng ta không thể thử trực tiếp được (vì tập số tự nhiên là vô hạn) thì ta có thể dùng Phương pháp quy nạp toán học để chứng minh.Bài làm mong đợi:n12345ĐúngĐúngĐúngĐúng
SaiĐúngĐúngĐúngĐúngĐúng Kể từ trở đi, sai, dường như vẫn đúng. Có thể khẳng định sai với nhưng không thể khẳng định đúng với .Hoạt động 3: Phương pháp quy nạp Toán học
Phương pháp quy nạp toán học:Bước 1: Kiểm tra mệnh đề đúng với .Bước 2: Giả sử mệnh đề đúng với (giả thiết quy nạp). Ta chứng minh mệnh đề cũng đúng với . Học sinh ghi chép bài
Hoạt động 4: Các ví dụ1. Ví dụ 1: Chứng minh rằng với thì (1)Giáo viên phát vấn hướng dẫn:- Vế trái có bao nhiêu số hạng?- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên hướng dẫn từng bước cho học sinh làm quen và làm bài.2. Ví dụ 2: Chứng minh rằng với thì (2)Giáo viên phát vấn hướng dẫn:- Vế trái có bao nhiêu số hạng?- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.3. Ví dụ 3: Chứng minh rằng với thì (3)Giáo viên phát vấn hướng dẫn:- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm ví dụ 1:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (1) đúng với . Tức là:Ta chứng minh (1) đúng với . Tức là:Thật vậy, ta có:Vậy (1) đúng với .Bài làm ví dụ 2:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (2) đúng với . Tức là:Ta chứng minh (2) đúng với . Tức là:Thật vậy, ta có:Vậy (2) đúng với .Bài làm ví dụ 3:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (3) đúng với . Tức là:Ta chứng minh (3) đúng với . Tức là:Thật vậy, ta có:Vậy (3) đúng với .Hoạt động 5: Chú ýGiáo viên nêu chú ý SGK:Nếu muốn chứng minh mệnh đề đúng với mọi số tự nhiên với p là số tự nhiên thì:Bước 1: Kiểm tra mệnh đề đúng với .Bước 2: Giả sử mệnh đề đúng với (giả thiết quy nạp). Ta chứng minh mệnh đề cũng đúng với . Học sinh ghi chép bài
Hoạt động 6: Cho hai số và với a. So sánh và với .b. Dự đoán kết quả và chứng minh bằng quy nạp.Giáo viên phát vấn hướng dẫn:- Kể từ giá trị n bằng bao nhiêu ta có bất đẳng thức ? Liệu bất đẳng thức có đúng kể từ n bằng giá trị đó trở đi không?- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm mong đợi:n12345392781243816243240 Dự đoán với số tự nhiên (*)Chứng minh:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (*) đúng với . Tức là:Ta chứng minh (*) đúng với . Tức là:Thật vậy, ta có:Vậy (*) đúng với .Hoạt động 7: Bài tập 1b SGK trang 82Giáo viên phát vấn hướng dẫn:- Vế trái có bao nhiêu số hạng?- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm mong đợi:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (*) đúng với . Tức là:Ta chứng minh (*) đúng với . Tức là:Thật vậy, ta có:Vậy (*) đúng với .Hoạt động 8: Bài tập 2a SGK trang 82Giáo viên phát vấn hướng dẫn:- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm mong đợi:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (*) đúng với . Tức là:Ta chứng minh (*) đúng với . Tức là:Thật vậy, ta có:Vậy (*) đúng với .Hoạt động 9: Bài tập 3a SGK trang 82Giáo viên phát vấn hướng dẫn:- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm mong đợi:Bước 1: Với , ta có: đúng.Bước 2: Giả sử (*) đúng với . Tức là:Ta chứng minh (*) đúng với . Tức là:Thật vậy, ta có:Vậy (*) đúng với .Hoạt động 10: Bài tập 4 SGK trang 83Giáo viên gọi 3 học sinh lên bảng tính , , .Giáo viên phát vấn hướng dẫn:- Từ kết quả của , , , em có thể dự đoán công thức của như thế nào?- Hãy nêu công thức cần chứng minh.- Bước 1 cần kiểm tra điều gì? Như thế nào?- Với bước 2, điều ta đã có là gì, điều là cần chứng minh là gì? Mệnh đề đúng với , đúng với nghĩa là như thế nào?
Giáo viên gọi một học sinh lên bảng làm bài, yêu cầu học sinh khác nhận xét, uốn nắn sửa sai và hoàn chỉnh bài làm cho học sinh.Bài làm mong đợi:a. , , b. Dự đoán: . Cần chứng minh: (*)Bước 1: Với , ta có: đúng.Bước 2: Giả sử (*) đúng với . Tức là:Ta chứng minh (*) đúng với . Tức là:Thật vậy, ta có:Vậy (*) đúng với .Hoạt động 11: Củng cố toàn bài1. Nội dung của phương pháp quy nạp toán học (gồm hai bước và bắt buộc theo trình tự nhất định).2. Nắm rõ các bước của phương pháp quy nạp..3. Dặn dò học sinh xem lại toàn bộ lý thuyết liên quan và làm lại toàn bộ bài tập đã sửa.4. Chuẩn bị Dãy số. V. Ghi chú:Tổ trưởng duyệt
Giáo viên
Huỳnh Đại Xuyên

Lý thuyết Phương pháp quy nạp toán học lớp 11 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 11 Bài 1: Phương pháp quy nạp toán học.

Lý thuyết Toán 11 Bài 1: Phương pháp quy nạp toán học

Bài giảng Toán 11 Bài 1: Phương pháp quy nạp toán học

A. Lý thuyết

I. Phương pháp quy nạp toán học

Để chứng minh những mệnh đề liên quan đến số tự nhiên là đúng với mọi n mà không thể thử trực tiếp được thì có thể làm như sau:

– Bước 1. Kiểm tra mệnh đề đúng với n = 1.

– Bước 2. Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1 (gọi là giả thiết quy nạp), chứng minh rằng nó cũng đúng với n = k + 1.

Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.

II. Ví dụ áp dụng

– Ví dụ 1. Chứng minh với mọi số tự nhiên n ≥ 1 ta có:

1  +  2+ 3+…+​ n= n(n+ ​1)2  (*)

Lời giải:

Bước 1: Với n = 1 ta có:

Vế trái = 1 và vế phải = 1

Vậy hệ thức đúng với n = 1.

Bước 2: Giả sử hệ thức đúng với một số tự nhiên bất kì n = k ≥ 1 tức là:

1  +  2+ 3+…+​ k=   k(k+ ​1)2  (1)

Ta cần chứng minh hệ thức đúng với n = k + 1, tức là:

1  +  2+ 3+…+​ k  +  k+​1= (k+​1)(k+ 2)2  (2)

Thật vậy:

Vế trái = 1 + 2 + 3+ … + k + k + 1

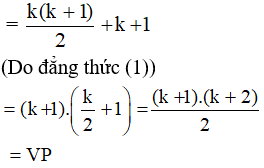
Vậy hệ thức đã cho đúng với mọi số tự nhiên n ≥ 1.

– Ví dụ 2. Chứng minh rằng với , ta có bất đẳng thức

1.3.5….(2n−1)2.4.6. . .2n     1 2n + 1

Lời giải:

– Với n = 1, bất đẳng thức cho trở thành:12     13 (đúng).

Vậy bất đẳng thức cho đúng với n = 1.

– Giả sử bất đẳng thức cho đúng với mọi số tự nhiên n = k ≥ 1, tức là :

1.3.5….(2k−1)2.4.6. . .2k     1 2k + 1 (1)

-Ta chứng minh bất đẳng thức cho đúng với n = k + 1, tức là :

1.3.5….(2k−1)(2k+​1)2.4.6. . .2k(2k+​ 2)     1 2k + 3 (2)

Thật vậy, ta có :

VT(2)= 1.3.5….(2k−1)2.4.6. . .2k. 2k+​12k+​2     1 2k + 1. 2k+​12k+​2  = 2k+ ​12k+​2 (theo (1))

Ta chứng minh:

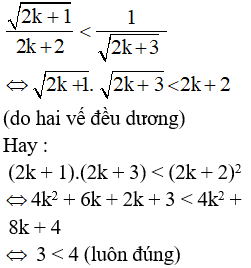
Vậy bất đẳng thức đã cho đúng với mọi số tự nhiên n ≥ 1.

– Chú ý:

Nếu phải chứng minh mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là một số tự nhiên) thì:

+ Ở bước 1, ta phải kiểm tra mệnh đề đúng với n = p;

+ Ở bước 2, ta giả thiết mệnh đề đúng với số tự nhiên bất kì n = k ≥ p và phải chứng minh rằng nó cũng đúng với n = k + 1.

B. Bài tập tự luyện

Bài 1. Với mỗi số nguyên dương n, chứng minh:

12 +​ 22 + 32+​ …+ ​n2  = n(n+​  1).(2n+​ 1)6

Lời giải:

– Với n = 1 thì vế trái = 12 = 1 và vế phải = 1(1+1)(2.1+1)6=1.

Vậy đẳng thức đúng với n = 1.

– Giả sử đẳng thức đúng với n = k ≥ 1, tức là:

12 +​ 22 + 32+​ …+ ​k2  = k(k+​  1).(2k+​ 1)6

– Ta chứng minh đẳng thức cũng đúng với n = k + 1, tức là chứng minh

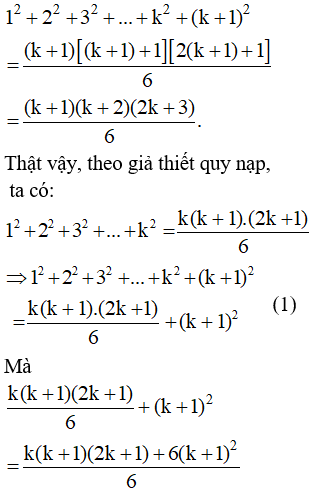
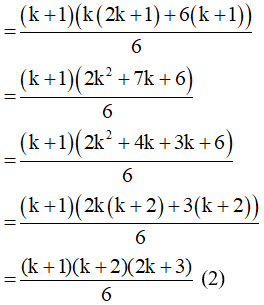
Từ (1); (2) suy ra

12+22+32+…+k2+(k+1)2=(k+1)(k+2)(2k+3)6.

Do đó đẳng thức đúng với n = k + 1. Suy ra có điều phải chứng minh.

Bài 2. Chứng minh rằng với mọi số tự nhiên n ≥ 4, ta có: 2n + 1 > n2 + 3n.

Lời giải:

Bước 1: Với n = 4 thì vế trái bằng 24 + 1 = 32 và vế phải bằng 42 + 3.4 = 28 .

Do 32 > 28 nên bất đẳng thức đúng với n = 4.

Bước 2: Giả sử đẳng thức đúng với n = k ≥ 4, nghĩa là 2k + 1 > k2 + 3k.

Ta chứng minh bất đẳng thức cũng đúng với n = k + 1, tức là phải chứng minh

2(k + 1) + 1 > (k + 1)2 + 3(k + 1) hay 2k + 2 > k2 + 5k + 4

Thật vậy, theo giả thiết quy nạp ta có 2k + 1 > k2 + 3k.

Suy ra, 2.2k + 1 > 2.(k2 + 3k) hay 2k + 2 > 2k2 + 6k.

Mặt khác: 2k2 + 6k – (k2 + 5k + 4) = k2 + k – 4 ≥ 42 + 4 – 3 = 16 với mọi k ≥ 4.

Do đó, 2k + 2 > 2k2 + 6k > k2 + 5k + 4 hay bất đẳng thức đúng với n = k + 1.

Suy ra bất đẳng thức được chứng minh.

Bài 3. Bằng phương pháp quy nạp toán học, chứng minh rằng 7n + 5 chia hết cho 6 với n ≥ 1.

Lời giải:

Thật vậy: Với n = 1 thì 71 + 5 = 12 ⁝ 6.

Giả sử mệnh đề đúng với n = k ≥ 1, nghĩa là 7k + 5 chia hết cho 6.

Ta chứng minh mệnh đề đúng với n = k + 1, nghĩa là phaỉ chứng minh 7k + 1 + 5 chia hết cho 6.

Ta có: 7k + 1 + 5 = 7(7k + 5) – 30.

Theo giả thiết quy nạp thì (7k + 5) ⁝ 6 nên 7(7k + 5) ⁝ 6

Lại có: 30 ⁝ 6 nên (7k + 1 + 5) ⁝ 6

Vậy 7n + 5 chia hết cho 6 với mọi n ≥ 1 .

Trắc nghiệm Toán 11 Bài 1: Phương pháp quy nạp toán học

Câu 1. Với mọi số tự nhiên n , tổng Sn=n3+3n2+5n+3chia hết cho:

A. 3

B. 4

C. 5

D. 7

Hiển thị đáp án

Đáp án: A

Giải thích:

Với n = 0 ta có:S0=3chia hết cho 3, ta chứng minh
Sn=n3+3n2+5n+3chia hết cho 3 với mọi số tự nhiên n.

Giả sử mệnh đề trên đúng đến n=k , tức là
Sk=k3+3k2+5k+3chia hết cho 3, ta chứng minh mệnh đề trên đúng đến n=k+1, tức là Sk+​1cũng chia hết cho 3.

Ta có:

Sk+1

=(k+1)3+3(k+1)2+5(k+1)+3

=k3+6k2+14k+12

=(k3+3k2+5k+3)+3(k2+3k+3)

Có:Sk=k3+3k2+5k+3chia hết cho 3 theo giả thiết quy nạp,3(k2+3k+3)⋮3, do đó
Sk+1⋮3

Vậy
Sn⋮3với mọi số tự nhiên n.

Câu 2. Giá trị của tổng là:

S=1−2+3−4+…−2n+(2n+1)

A. 1

B. 0

C. 5

D. n +1

Hiển thị đáp án

Đáp án: D

Giải thích:

Với=0 ta có:S=1

Với=1ta có
S=1–2+3=2

Với=2ta có
S=1–2+3–4+5=3

Dự đoán S = n+1* ta sẽ chứng minh *đúng bằng quy nạp.

Với n = 0 đương nhiên*đúng.

Giả sử*đúng vớin=k, tức là

Sk=1−2+3−4+…−2k+(2k+1)

=k+1, ta chứng minh*đúng vớin=k+1.

Ta có:

Sk+1=1−2+3−4+…2(k−1)

+(2(k+1)+1)

=(1−2+3−4+…−2k+2k+1)

−(2k+2)+(2k+3)

=Sk−(2k+2)+(2k+3)

=k+1−2k−2+​2k+3

=k+​2

Vậy* đúng với mọi số tự nhiên n, tức là S = n+1.

Câu 3. Với mọi số nguyên dương n , tổng Sn=1.2+2.3+3.4+…+n(n+1) là:

A.n(n+1)(n+2)(n+3)6

B.n(n+1)(n+2)3

C.n(n+1)(n+2)2

D. Đáp số khác

Hiển thị đáp án

Đáp án: B

Giải thích:

Với =1 ta có: S =1.2=2, do đó đáp án A, C sai.

Ta chứng minh
Sn=n(n+1)(n+2)3(*)đúng với mọi số nguyên dương.

Giả sử*đúng đến, tức là

Sk=1.2+2.3+3.4+…+k(k+1)

=k(k+1)(k+2)3

, ta chứng minh (∗) đúng đếnn=k+1, tức là cần chứng minh

Sk+1

=1.2+2.3+…+(k+1)(k+2)

=(k+1)(k+2)(k+3)3

Ta có:

Sk+1=1.2+2.3+…+k(k+1)+(k+1)(k+2)=k(k+1)(k+2)3+(k+1)(k+2)=  (​k​+1).k2+​2k3+​k+2=(k+1)(k2+2k+3k+6)3=(k+1)(k2+5k+6)3=(k+1)(k+2)(k+3)3

Vậy* đúng với mọi số nguyên dương n.

Câu 4: Một học sinh chứng minh mệnh đề “”8n+1 chia hết cho 7,∀n∈N*””(*) như sau:

Giả sử *đúng với n=ktức là 8k+ 1 chia hết cho 7

Ta có: 8k+ 1 = 8(8k+1)- 7, kết hợp với giả thiết 8k+ 1 chia hết cho 7 nên suy ra được 8k+1+ 1 chia hết cho 7.

Vậy đẳng thức * đúng với mọin∈N*

Khẳng định nào sau đây là đúng?

A. Học sinh trên chứng minh đúng.

B. Học sinh chứng minh sai vì không có giả thiết qui nạp.

C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.

D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp

Hiển thị đáp án

Đáp án: D

Giải thích:

Quan sát lời giải trên ta thấy:

Học sinh thực hiện thiếu bước 1: Kiểm tran=1 thì81+1=9 không chia hết cho7nên mệnh đề đó sai.

Câu 5: Với n∈N*, ta xét các mệnh đề: P:“ 7n+ 5 chia hết cho 2”;

Q: “7n+ 5 chia hết cho 3” và R: “7n+ 5 chia hết cho 6”.

Số mệnh đề đúng trong các mệnh đề trên là:

A. 3

B. 0

C. 1

D. 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Bằng quy nạp toán học ta chứng minh được7n+ 5 chia hết cho6.

Thật vậy, với n = 1 ta có:71+ 5 =12 ⋮6

Giả sử mệnh đề đúng với n = k , nghĩa là7k+ 5 chia hết cho 6, ta chứng minh mệnh đề cũng đúng với , nghĩa là phải chứng minh7k+1+ 5 chia hết cho 6.

Ta có:7k+1+ 5 =7(7k+5)−30

Theo giả thiết quy nạp ta có7k+5chia hết cho6, và30chia hết cho6nên

7(7k+5)−30cũng chia hết cho6.

Do đó mệnh đề đúng vớin=k+1.

Vậy7n+ 5 chi hết cho6với mọin∈N*

Mọi số chia hết cho6đều chia hết cho2và chia hết cho3.

Do đó cả 3 mệnh đề đều đúng.

Câu 6: Trong phương pháp quy nạp toán học, nếu ta giả sử mệnh đề đúng với n=kthì ta cần chứng minh mệnh đề đúng đến:

A.n=k−1

B.n=k−2

C.n=k+1

D.n=k+2

Hiển thị đáp án

Câu 7: Đối với bài toán chứng minh P(n)đúng với mọi n≥p với p là số tự nhiên cho trước thì ở bước 1 ta cần chứng minh mệnh đề đúng với:

A.n=1

B.n=k

C.n=k+1

D.n=p

Hiển thị đáp án

Đáp án: D

Giải thích:

Đối với bài toán chứng minh
P(n) đúng với mọin≥p với p là số tự nhiên cho trước thì:

– Bước 1: Chứng minh
P(n)đúng vớin=p

– Bước 2: Vớik≥plà một số nguyên dương tùy ý, giả sử
P(n) đúng vớin=k, chứng minh
P(n) cũng đúng khin=k+1.

Từ đó ta thấy, ở bước đầu tiên ta cần chứng minh mệnh đề đúng vớin=p chứ không phảin=1.

Câu 8: Dùng quy nạp chứng minh mệnh đề chứa biến P(n) đúng với mọi số tự nhiên n≥p (p là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề P(n)đúng với n=k. Khẳng định nào sau đây là đúng?

A.k≠p

B.k≥p

C.k=p

D.kp

Hiển thị đáp án

Câu 9: Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến đúng với mọi số tự nhiên n≥p ( p là một số tự nhiên), ta tiến hành hai bước:

– Bước 1, kiểm tra mệnh đề P(n) đúng vớin=p

– Bước 2, giả thiết mệnh đề P(n)đúng với số tự nhiên bất kỳ n=k≥p và phải chứng minh rằng nó cũng đúng với n=k+1

Trong hai bước trên:

A. Chỉ có bước 1 đúng.

B. Chỉ có bước 2 đúng.

C. Cả hai bước đều đúng

D. Cả hai bước đều sai

Hiển thị đáp án

Đáp án: C

Giải thích:

Đối với bài toán chứng minh
P(n)đúng với mọin≥p vớiplà số tự nhiên cho trước thì:

– Bước 1: Chứng minh
P(n)đúng vớin=p.

– Bước 2: Vớilà một số nguyên dương tùy ý, giả sửđúng với, chứng minhcũng đúng khin=k+1.

Từ lý thuyết trên ta thấy cả hai bước trên đều đúng.

Câu 10: Trong phương pháp quy nạp toán học, ở bước 2, nếu ta giả sử mệnh đề đúng với n=k+1thì ta cần chứng minh mệnh đề đúng với:

A.n=k

B.n=k+1

C.n=k+2

D.n=k+3

Hiển thị đáp án

Đáp án: B

Giải thích:

Phương pháp quy nạp toán học:

– Bước 1: Chứng minh
P(n) đúng vớin=1.

Xem thêm:

– Bước 2: Vớiklà một số nguyên dương tùy ý, giả sử
P(n)đúng vớin=k, chứng minh
P(n)cũng đúng khin=k+1.

Do đó ta thấy, ở bước 2, nếu ta giả sử mệnh đề đúng vớithì ta cần chứng minh mệnh đề đúng với1