Đại số 10 năm 2023 (mới nhất), giáo án toán 10 năm 2023 (mới nhất)

Lớp 1

Đề thi lớp 1

Lớp 2

Lớp 2 – Kết nối tri thức

Lớp 2 – Chân trời sáng tạo

Lớp 2 – Cánh diều

Tài liệu tham khảo

Lớp 3

Lớp 3 – Kết nối tri thức

Lớp 3 – Chân trời sáng tạo

Lớp 3 – Cánh diều

Tài liệu tham khảo

Lớp 4

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Lớp 5

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Lớp 6

Lớp 6 – Kết nối tri thức

Lớp 6 – Chân trời sáng tạo

Lớp 6 – Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 7

Lớp 7 – Kết nối tri thức

Lớp 7 – Chân trời sáng tạo

Lớp 7 – Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 8

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 9

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 10

Lớp 10 – Kết nối tri thức

Lớp 10 – Chân trời sáng tạo

Lớp 10 – Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 11

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 12

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

IT

Ngữ pháp Tiếng Anh

Lập trình Java

Phát triển web

Lập trình C, C++, Python

Cơ sở dữ liệu

Giáo án Toán 10 năm 2023 (mới nhất) | Giáo án Toán 10 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

Với mục đích giúp các Thầy / Cô dễ dàng biên soạn Giáo án Toán 10, Viet
Jack biên soạn bộ Giáo án Toán 10 Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ Học kì 1 & Học kì 2 phương pháp mới theo hướng phát triển năng lực bám sát mẫu giáo án của BGD. Hi vọng tài liệu Giáo án Toán 10 này sẽ được Thầy/Cô đón nhận và đóng góp những ý kiến quí báu.

Bạn đang xem: Đại số 10 năm 2023 (mới nhất)

Mục lục Giáo án Toán 10 năm 2023 (cả ba sách)

Xem thử Giáo án Toán 10 KNTTXem thử Giáo án Toán 10 CTSTXem thử Giáo án Toán 10 CD

Chỉ 250k mua trọn bộ Giáo án Toán 10 cả năm (mỗi bộ sách) bản word chuẩn kiến thức, trình bày đẹp mắt:

Lưu trữ: Giáo án Toán 10 (sách cũ)

Tải xuống

Giáo án Toán lớp 10 Đại số

Giáo án Toán 10 Chương 1: Mệnh đề – Tập hợp

Giáo án Toán 10 Chương 2: Hàm số bậc nhất và bậc hai

Giáo án Toán 10 Chương 3: Phương trình. Hệ phương trình

Giáo án Toán 10 Chương 4: Bất đẳng thức. Bất phương trình

Giáo án Toán 10 Chương 5: Thống kê

Giáo án Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác

Giáo án Toán lớp 10 Học kì 1

Giáo án Toán lớp 10 Học kì 2

Giáo án Toán lớp 10 Hình học

Giáo án Toán 10 Chương 1: Vectơ

Giáo án Toán 10 Chương 2: Tích vô hướng của hai vectơ và ứng dụng

Giáo án Toán 10 Chương 3: Phương pháp tọa độ trong mặt phẳng

Giáo án Toán 10 Bài 1: Mệnh đề

A. KẾ HOẠCH CHUNG

Tiết 1	HOẠT ĐỘNG KHỞ I ĐỘNG
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC	Mệnh đề, Mệnh đề chứa biến
Tiết 2	Mệnh đề phủ định
Mệnh đề kéo theo
Mệnh đề đảo, hai mệnh đề tương đương
Kí hiệu ∀ và ∃
Tiết 3	HOẠT ĐỘNG LUYỆN TẬPHOẠT ĐỘNG VẬN DỤNGHOẠT ĐỘNG TÌM TÒI, MỞ RỘNG

B. KẾ HOẠCH DẠY HỌC

I. MỤC TIÊU

1. Về kiến thức

– Biết thế nào là một mệnh đề, mệnh đề phủ định, mệnh đề chứa biến.

– Biết ký hiệu phổ biến ∀, kí hiệu ∃

– Biết được mệnh đề kéo theo, mệnh đề tương đương.

– Phân biệt được điều kiện cần, điều kiện đủ, giả thiết và kết luận.

2.Về kĩ năng

– Biết lấy Ví dụ về mệnh đề, mệnh đề phủ định của một mệnh đề, xác định được tính đúng sai của mệnh đề trong những trường hợp đơn giản.

– Nêu được Ví dụ mệnh đề kéo theo và mệnh đề tương đương.

– Biết được mệnh đề đảo của một mệnh đề cho trước.

3.Về tư duy, thái độ

– Rèn tư duy logic , thái độ nghiêm túc.

– Tích cực, chủ động, tự giác trong chiếm lĩnh kiến thức, trả lời các câu hỏi.

– Tư duy sáng tạo.

4. Định hướng phát triển năng lực cho học sinh

– Năng lực chung:

+ Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điều chỉnh được kế hoạch học tập; tự nhận ra được sai sót và cách khắc phục sai sót.

+ Năng lực giải quyết vấn đề : Biết tiếp nhận câu hỏi, bài tập có vấn đề hoặc đặt ra câu hỏi. Phân tích được các tình huống trong học tập.

+ Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập vào trong cuộc sống; trưởng nhóm biết quản lý nhóm mình,

phân công nhiệm vụ cụ thể cho từng thành viên nhóm, các thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhiệm vụ được giao.

+ Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.

+ Năng lực hợp tác: Xác định nhiệm vụ của nhóm, trách nhiệm của bản thân đưa ra ý kiến đóng góp hoàn thành nhiệm vụ của chủ đề.

+ Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học .

+ Năng lực sử dụng công nghệ thông tin và truyền thông

– Năng lực chuyên biệt:

+ Năng lực tự học: Đọc trước và nghiên cứu chủ đề qua nội dung bài trong sách giáo khoa Đại số lớp 10 (Ban cơ bản).

+ Năng lực giải quyết vấn đề.

+ Năng lực sử dụng ngôn ngữ.

II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH

1. Chuẩn bị của GV

+/ Soạn KHBH

+/ Chuẩn bị phương tiện dạy học: Phấn, thước kẻ, máy chiếu…

2. Chuẩn bị của HS

+/ Đọc trước bài

+/ Kê bàn để ngồi học theo nhóm

+/ Chuẩn bị bảng phụ, bút viết bảng, khăn lau bảng …

III. MÔ TẢ CÁC MỨC ĐỘ

Nội dungNhận thứcThông hiểuVận dụngVận dụng cao

Mệnh đề. Mệnh đề chứa biến	– Hiểu được câu nào là mệnh đề, câu nào không phải là mệnh đề. – Hiểu được thế nào là mệnh đề chứa biến. – Phân biệt được được mệnh đề và mệnh đề chứa biến.	– Lấy được Ví dụ về mệnh đề, mệnh đề chứa biến. – Xác định được giá trị đúng, sai của một mệnh đề. – Biết gán giá trị cho biến và xác định tính đúng, sai.
Phủ định của một mệnh đề	– Hiểu được mệnh đề phủ định và kí hiệu. – Xác định được tính đúng, sai của mệnh đề.	Lập được mệnh đề phủ định
Mệnh đề kéo theo	– Hiểu được khái niệm mệnh đề kéo theo. – Xác định trong định lý đâu là điều kiện cần, điều kiện đủ	– Lập được mệnh đề kéo theo khi biết trước hai mệnh đề liên quan. -Phát biểu định lý Toán học dưới dạng mệnh đề kéo theo	– Xác định được tính đúng sai của mệnh đề kéo theo. – Phát biểu được định lý Toán học dưới dạng điều kiện cần, điều kiện đủ.
Mệnh đề đảo hai mệnh đề tương đương	Hiểu được khái niệm mệnh đề đảo, hai mệnh đề tương đương.	– Lập được mệnh đề đảo của mệnh đề, của một mệnh đề kéo theo cho trước.	– Xác định được tính Đúng, Sai của mệnh đề: kéo theo, mệnh đề đảo. – Phát biểu được hai mệnh đề tương đương dưới ba dạng: tương đương; điều kiện cần, điều kiện đủ; khi và chỉ khi.
Kí hiệu ∀ , ∃	Hiểu được ý nghĩa cách đọc của hai kí hiệu ∀ , ∃	Lập được mệnh đề chứa hai kí hiệu ∀ , ∃	Lập được mệnh đề phủ định của mệnh đề chứa hai kí hiệu ∀ , ∃	Xác định được tính đúng, sai của mệnh đề chứa kí hiệu ∀ , ∃

IV. THIẾT KẾ CÂU HỎI /BÀI TẬP THEO CÁC MỨC ĐỘ

Mức độ

Nội dung

Câu hỏi/ bài tập

Nhận biết

Vận dụng

Mệnh đề. Mệnh đề chứa biến	Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? 1) Văn hóa cồng chiêng là di sản văn hóa phi vật thể của Thế giới. 2) π2 Thông hiểu	Mệnh đề. Mệnh đề chứa biến
Phủ định của một mệnh đề
Mệnh đề kéo theo	+ Vận dụng: ( HĐ nhóm ) 1/ HĐ 5: cho P : “gió đông bắc về”, Q : “Trời trở lạnh” Hãy phát biểu mệnh đề P ⇒ Q? 2/ Cho 1 ví dụ về mệnh đề kéo theo? +Nêu giả thiết, kết luận, điều kiện cần, điều kiện đủ?
Mệnh đề đảo hai mệnh đề tương đương
Kí hiệu ∀ , ∃
Mệnh đề. Mệnh đề chứa biến	Vận dụng: Xét câu: “x > 3” hãy tìm hai giá trị thực của x để từ câu đã cho nhận được một mệnh đề đúng, một mệnh đề sai. Cho ví dụ về mệnh đề chứa biến?
Phủ định của một mệnh đề	HĐ 4: Hãy phủ định các mệnh đề sau •P: “ là một số hữu tỉ”. •Q: “Tổng hai cạnh của tam giác lớn hơn cạnh thứ ba” Xét tính đúng sai của các mệnh đề trên và mệnh đề phủ định.
Mệnh đề kéo theo	+Vận dụng: ( HĐ nhóm ) HĐ 6 (SGK): Cho tam giác ABC. Xét mệnh đề P: “tam giác ABC có hai góc bằng 600> Q: “ABC là một tam giác đều” Phát biều định lí ⇒ Nêu giả thiết, kết luận và phát biểu định lý dưới dạng điều kiện cần, điều kiện đủ.
Mệnh đề đảo hai mệnh đề tương đương
Kí hiệu ∀ , ∃	+Vận dụng: HĐ nhóm 1/ Viết gọn câu : Có 1 số tự nhiên n mà 2n=1 2/ Phủ định “ ∀n∈N*, n2 -1 là bội của 3” “∃x∈Q ,x2=3 ” 3/ Phủ định: “Tất cả các bạn trong lớp em đều có máy tính”

V. TIẾN TRÌNH DẠY HỌC

HOẠT ĐỘNG KHỞ
I ĐỘNG

1. Mục tiêu :

+ Hình thành khái niệm về mệnh đề ; các phép toán trên mệnh đề.

+ Hình thành khái niệm tập hợp, Các phép toán tập hợp.

+ Sai số, số gần đúng.

2. Nội dung và phương pháp thực hiện.

*Chuyển giao nhiệm vụ :

Hãy chỉ ra các câu sau, câu nào là câu khẳng định, câu khẳng định có giá trị đúng, câu khẳng định có giá trị sai.

1) Văn hóa cồng chiêng là di sản văn hóa phi vật thể của Thế giới.

2)π2 * Thực hiện nhiệm vụ : Trình bày sản phẩm ra bảng phụ.

* Báo cáo và thảo luận : Một HS đại diện cho nhóm trình bày, nhóm khác theo dõi và ra câu hỏi thảo luận

3. Sản phẩm :

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC MỚI

HOẠT ĐỘNG 1: Mệnh đề, mệnh đề chứa biến

Mục tiêu: Đưa ra khái niệm mệnh đề, mệnh đề chứa biến.

HS lấy các ví dụ về mệnh đề, mệnh đề chứa biến

Nội dung và phương thức thực hiện:

Từ ví dụ tên HS hãy đưa ra khái niệm mệnh đề, mệnh đề chứa biến và lấy ví dụ minh họa.

HS phát biểu khái niệm về mệnh đề, mện đề chứa biến. Lấy ví dụ về mệnh đề.

HS theo dõi câu trả lời của bạn và nhận xét, chốt kiến thức.

Chốt KT: Mệnh đề là 1 câu khẳng định 1 vấn đề nào đó, mệnh đề nhận một giá trị đúng hoặc sai, mệnh đề không vừa đúng vừa sai.

Tính đúng sai của mệnh đề chứa biến phụ thuộc vào giá trị của biến

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

Giáo án Toán 10 Bài 2: Tập hợp

I. MỤC TIÊU

1. Về kiến thức

– Hiểu được khái niệm tập hợp, tập hợp con, hai tập hợp bằng nhau.

2.Về kĩ năng

– Sử dụng được các kí hiệu: ∈;∉;⊂;⊃;∅

– Biết biểu diễn tập hợp bằng hai cách: Liệt kê các phần tử của tập hợp hoặc chỉ ra tính chất đặc trưng của tập hợp

– Vận dụng các khái niệm tập hợp con, tập hợp bằng nhau vào giải toán

– Thực hiện được các phép toán lấy giao của hai tập hợp, hợp của hai tập hợp, phần bù của một tập con

3.Về tư duy, thái độ

– Rèn tư duy logic , thái độ nghiêm túc.

– Tích cực, chủ động, tự giác trong chiếm lĩnh kiến thức, trả lời các câu hỏi.

– Tư duy sáng tạo.

4. Định hướng phát triển năng lực cho học sinh

– Năng lực chung:

+ Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điều chỉnh được kế hoạch học tập; tự nhận ra được sai sót và cách khắc phục sai sót.

+ Năng lực giải quyết vấn đề : Biết tiếp nhận câu hỏi, bài tập có vấn đề hoặc đặt ra câu hỏi. Phân tích được các tình huống trong học tập.

+ Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập vào trong cuộc sống; trưởng nhóm biết quản lý nhóm mình, phân công nhiệm vụ cụ thể cho từng thành viên nhóm, các thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhiệm vụ được giao.

+ Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.

+ Năng lực hợp tác: Xác định nhiệm vụ của nhóm, trách nhiệm của bản thân đưa ra ý kiến đóng góp hoàn thành nhiệm vụ của chủ đề.

+ Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học .

+ Năng lực sử dụng công nghệ thông tin và truyền thông

– Năng lực chuyên biệt:

+ Năng lực tự học: Đọc trước và nghiên cứu chủ đề qua nội dung bài trong sách giáo khoa Đại số lớp 10 (Ban cơ bản).

+ Năng lực giải quyết vấn đề.

+ Năng lực sử dụng ngôn ngữ.

II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH

1. Chuẩn bị của GV

+/ Soạn KHBH

+/ Chuẩn bị phương tiện dạy học: Phấn, thước kẻ, máy chiếu…

2. Chuẩn bị của HS

+/ Đọc trước bài

+/ Kê bàn để ngồi học theo nhóm

+/ Chuẩn bị bảng phụ, bút viết bảng, khăn lau bảng …

III. MÔ TẢ CÁC MỨC ĐỘ

Nội dungNhận thứcThông hiểuVận dụngVận dụng cao

Tập hợp và phần tử	Học sinh nắm được khái niệm tập hợp	Học sinh lấy được ví dụ về tập hợp,số phần tử của tập hợp,biết sử dụng kí hiệu ∈;∉
Cách xác định tập hợp	Học sinh biết được xác định tập hợp có mấy cách	Học sinh sử dụng được hai cách để xác định một tập hợp	Học sinh liệt kê được các phần tử của một tập hợp	Học sinh chỉ ra được tính chất đặc trưng của một tập hợp cho trước
Tập rỗng	Học sinh nắm được định nghĩa Học sinh biết sử dụng các kí hiệu ∈;∉;∅
Tập hợp con	Học sinh nắm được khái niệm tập con	Học sinh hiểu được khái niệm tập con. Sử dụng được các kí hiệu ⊂;⊃ .	Học sinh xác định được tập con của một tập hợp.	Học sinh chứng minh được tập này là con của tập kia.
Tập hợp bằng nhau	Nắm được khái niệm hai tập hợp bằng nhau	Hiểu được khái niệm hai tập hợp bằng nhau.	Xác định được hai tập hợp bằng nhau	Chứng minh được hai tập hợp bằng nhau.

IV. TIẾN TRÌNH DẠY HỌC

A. HOẠT ĐỘNG KHỞ
I ĐỘNG

1. Mục tiêu:

+ Hình thành khái niệm tập hợp.

2. Nội dung và phương pháp thực hiện.

*Chuyển giao nhiệm vụ :

Liệt kê tên các bạn trong bàn mình đang ngồi, trong nhóm của mình, đưa ra nhận xét mối quan hệ của các bạn trong bàn với trong nhóm.

* Thực hiện nhiệm vụ : Trình bày sản phẩm ra bảng phụ.

* Báo cáo và thảo luận : Một HS đại diện cho nhóm trình bày, nhóm khác theo dõi và ra câu hỏi thảo luận

* Chốt kiến thức :

B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC MỚI

HĐ1: Tập hợp

-Mục tiêu: tiếp cận khái niệm tập hợp, cách xác định tập hợp

-Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh làm việc cá nhân giải quyết vấn đề sau:

CÂU HỎIGỢI Ý

H1: Hãy cho ví dụ về một vài tập hợp? H2: Liệt kê các phần tử của tập hợp B là ước cả 30 Cho tập hợp A = {x ∈ R/ x2- 3x +2=0}. Liệt kê các phần tử của tập hợp H3:Biểu diễn tập hợp B bằng biểu đồ ven	G1: Tập hợp những viên phấn trong hộp phấn. mỗi viên phấn là một phần tử của tập hợp G2: B={1,2,3,5,6,10,15,30} G3:

+ Thực hiện: Học sinh suy nghĩ và làm ví dụ vào giấy nháp.+ Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó nêu cách xác định tập hợp và các chú ý. HS viết bài vào vở.

NỘI DUNG GHI BẢNG

I. KHÁI NIỆM TẬP HỢP 1. Tập hợp và phần tử VD : -Tập hợp các HS lớp 10A5 -Tập hợp những viên phấn trong hộp phấn -Tập hợp các số tự nhiên *Nếu a là phần tử của tập X, KH: a∈ X (a thuộc X) *Nếu a không là phần tử của tập X , KH :a ∉ X (a không thuộc X)

2. Cách xác định tập hợp Cách 1 : Liệt kê các phần tử của tập hợp Cách 2 : Chỉ rõ các tính chất đặc trưng cho các phần tử của tập hợp +Minh họa tập hợp bằng biểu đồ ven: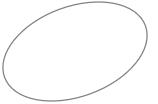

3. Tập hợp rỗng: Là tập hợp không chứa phần tử nào. KH ∅;

HĐ2. TẬP HỢP CON, TẬP HỢP BẰNG NHAU

Mục tiêu: tiếp nhận khái niệm tập hợp con, tập hợp bằng nhau

Nội dung, phương thức tổ chức:

+ Chuyển giao:Học sinh làm việc cá nhân giải quyết vấn đề sau:

CÂU HỎIGỢI Ý

H1:Thực hành hoạt động 5 trong sách giáo khoa H2:Xét 2 tập hợp A={ n∈N/n là bội của 4 và 6} B={n∈N/n là bội của 12} Hãy kiểm tra A⊂B; b⊂A	G1: có G2: A⊂B; b⊂A

+ Thực hiện: HS làm việc theo cặp đôi, viết lời giải vào giấy nháp. GV quan sát HS làm việc, nhăc nhở các em không tích cực, giải đáp nếu các em có thắc mắc về nội dung bài tập.

+ Báo cáo, thảo luận: Hết thời gian dự kiến cho từng bài tập, quan sát thấy em nào có lời giải tốt nhất thì gọi lên bảng trình bày lời giải. Các HS khác quan sát lời giải, so sánh với lời giải của mình, cho ý kiến.

+ Đánh giá, nhận xét, tổng hợp: GV chỉnh sửa, hoàn thiện lời giải trên bảng.Yêu cầu HS chép lời giải vào vở.

NỘI DUNG GHI BẢNG

II. Tập hợp con *ĐN : (SGK) A⊂B ⟺ (∀x, x∈A ⇒ x∈B) */Ta còn viết: A⊂B bằng cách B⊃A */Tính chất A⊂(B và B⊂C)⇒(A⊂C) A⊂A, ∀A ∅⊂A, ∀A +Biểu đồ Ven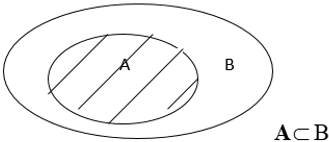

II. Tập Hợp Bằng Nhau Định nghĩa: A=B ⟺ A⊂B và B⊂A Vậy A=B ⟺ ∀x, x∈A ⟺ x∈B Hai tập bằng nhau gồm cùng các phần tử như nhau

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

Giáo án Toán 10 Bài 1: Các định nghĩa

A. KẾ HOẠCH CHUNG

Phân phối thời gian	Tiến trình dạy học
Tiết 1	HOẠT ĐỘNG TIẾP CẬN BÀI HỌC
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC	Định nghĩa vectơ
Vectơ cùng phương, Vectơ cùng hướng
Hai vectơ bằng nhau
Tiết 2	Vectơ – không
HOẠT ĐỘNG LUYỆN TẬP
HOẠT ĐỘNG VẬN DỤNG
HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG

B. KẾ HOẠCH DẠY HỌC

I. MỤC TIÊU CỦA BÀI:

1. Kiến thức:

– Nắm được định nghĩa vectơ và những khái niệm quan trọng liên quan đến vectơ như: sự cùng phương của hai vectơ, độ dài của vectơ, hai vectơ bằng nhau, …

– Hiểu được vectơ là một vectơ đặc biệt và những qui ước về vectơ .

2. Kĩ năng:

– Biết chứng minh hai vectơ bằng nhau, biết dựng một vectơ bằng vectơ cho trước và có điểm đầu cho trước.

3. Thái độ:

– Rèn luyện óc quan sát, phân biệt được các đối tượng.

4. Định hướng năng lực được hình thành:

– Biết quy lạ về quen, tư duy các vấn đề toán học một cách lo-gic

II. CHUẨN BỊ:

Giáo viên: Giáo án, phiếu học tập.

Học sinh: SGK, vở ghi. Đọc trước bài học.

III. CHUỖI CÁC HOẠT ĐỘNG HỌC :

1.Hoạt động tiếp cận bài học:

• Cho HS quan sát hình 1.1. Nhận xét về hướng chuyển động của ôtô và máy bay.

2. Hoạt động hình thành kiến thức bài học.

2.1. Định nghĩa vectơ.

a) Tiếp cận.

– Cho đoạn thẳng AB. Nếu ta chọn điểm A là điểm đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là đoạn thẳng có hướng. Từ đó hình thành khái niệm vectơ.

b) Hình thành

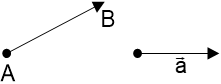I. Khái niệm vectơ ĐN: Vectơ là một đoạn thẳng có hướng. có điểm đầu là A, điểm cuối là B. Vectơ còn được kí hiệu là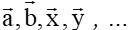

c) Củng cố:

H1. Với 2 điểm A, B phân biệt có bao nhiêu vectơ có điểm đầu và điểm cuối là A hoặc B?

2.2. Vectơ cùng phương, vectơ cùng hướng.

a) Tiếp cận.

• Cho HS quan sát hình 1.3. Nhận xét về giá của các vectơ

H1. Hãy chỉ ra giá của các vectơ:

, …?

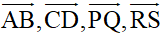
H2. Nhận xét về VTTĐ của các giá của các cặp vectơ:

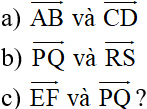
b) Hình thành

• Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ đgl giá của vectơ đó.

ĐN: Hai vectơ đgl cùng phương nếu giá của chúng song song hoặc trùng nhau.

• Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng.

• Ba điểm phân biệt A, B, C thẳng hàng ⇔ và cùng phương.

c) Củng cố:

• Nhấn mạnh các khái niệm: vectơ, hai vectơ phương, hai vectơ cùng hướng.

Ví dụ 1: Cho hbh ABCD. Chỉ ra các cặp vectơ cùng phương, cùng hướng, ngược hướng?

Ví dụ 2: Cho hai vectơ và cùng phương với nhau. Hãy chọn câu trả lời đúng:

A. cùng hướng với

B. A, B, C, D thẳng hàng

C. cùng phương với

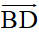
D.

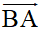
cùng phương với

2.3. Hai vectơ bằng nhau:

a) Tiếp cận.

GV giới thiệu khái niệm hai vectơ bằng nhau.

b) Hình thành

Hai vectơ bằng nhau: Hai vectơ

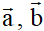
đgl bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu

.

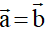
Chú ý: Cho

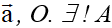
sao cho

.

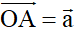
c) Củng cố:

Ví dụ 1. Cho hbh ABCD. Chỉ ra các cặp vectơ bằng nhau? Ví dụ 2. Cho tam giác ABC đều. 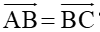? Ví dụ 3. Gọi O là tâm của hình lục giác đều ABCDEF. 1) Hãy chỉ ra các vectơ bằng 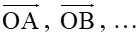? 2) Đẳng thức nào sau đây là đúng?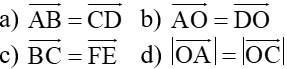

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

………………………………………………………………………………………..

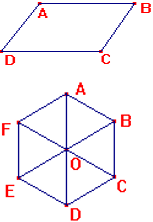Xem thử Giáo án Toán 10 KNTTXem thử Giáo án Toán 10 CTSTXem thử Giáo án Toán 10 CD

Tài liệu gồm 567 trang, được biên soạn bởi thầy giáo Trần Đình Cư, tổng hợp đầy đủ lý thuyết, các dạng toán và bài tập từ cơ bản đến nâng cao các chuyên đề Toán lớp 10 phần Đại số.

Khái quát nội dung tài liệu bài giảng cơ bản và nâng cao Toán 10 (Tập 1: Đại số 10):CHƯƠNG 1. MỆNH ĐỀ – TẬP HỢP.BÀI 1. MỆNH ĐỀ.Dạng 1. Nhận biết mệnh đề, mệnh đề chứa biến.Dạng 2. Xét tính đúng sai của mệnh đề.Dạng 3. Phủ định của mệnh đề.Dạng 4. Mệnh đề kéo theo, mệnh đề đảo và hai mệnh đề tương đương.Dạng 5. Mệnh đề với kí hiệu với mọi, tồn tại.BÀI 2. TẬP HỢP.Dạng 1. Tập hợp và các phần tử của tập hợp.Dạng 2. Tập hợp con và hai tập hợp bằng nhau.BÀI 3. CÁC PHÉP TOÁN TẬP HỢP.Dạng 1. Giao và hợp của hai tập hợp.Dạng 2. Hiệu và phần bù của hai tập hợp.Dạng 3. Bài toán sử dụng biểu đồ Ven.Dạng 4. Chứng minh X ⊂ Y. Chứng minh X = Y.BÀI 4. CÁC TẬP HỢP SỐ.Dạng 1. Tìm giao và hợp các khoảng, nửa khoảng, đoạn.Dạng 2. Xác định hiệu và phần bù các khoảng, đoạn, nửa khoảng.BÀI 5. SỐ GẦN ĐÚNG VÀ SAI SỐ.Dạng 1. Biết số gần đúng a và độ chính xác d. Ước lượng sai số tương đối, các chữ số chắc, viết dưới dạng chuẩn.Dạng 2. Biết số gần đúng a và sai số tương đối không vượt quá c. Ước lượng sai số tuyệt đối, các chữ số chắc, viết dưới dạng chuẩn.Dạng 3. Quy tròn số. Ước lượng sai số tuyệt đối, sai số tương đối của số quy tròn.Dạng 4. Sai số của tổng, tích và thương.Dạng 5. Xác định các chữ số chắc của một số gần đúng, dạng chuẩn của chữ số gần đúng và kí hiệu khoa học của một số.

CHƯƠNG 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI.BÀI 1. ĐẠI CƯƠNG VỀ HÀM SỐ.Dạng 1. Tính giá trị của hàm số tại một điểm.Dạng 2. Tìm tập xác định của hàm số.Dạng 3. Tính đồng biến, nghịch biến của hàm số.Dạng 4. Dựa vào đồ thị tìm các khoảng đồng biến, nghịch biến.Dạng 5. Xét tính chẵn lẻ của hàm số.BÀI 2. HÀM SỐ BẬC NHẤT.Dạng 1. Xét tính đồng biến, nghịch biến của hàm số.Dạng 2. Đồ thị hàm số bậc nhất.Dạng 3. Vị trí tương đối của hai đường thẳng.Dạng 4. Xác định hàm số bậc nhất.Dạng 5. Bài toán thực tế.BÀI 3. HÀM SỐ BẬC HAI.Dạng 1. Bảng biến thiên, tính đơn điệu, GTLN và GTNN của hàm số.Dạng 2. Xác định hàm số bậc hai.Dạng 3. Đồ thị hàm số bậc hai.Dạng 4. Sự tương giao.Dạng 5. Toán thực tế.

CHƯƠNG 3. PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH.BÀI 1. ĐẠI CƯƠNG VỀ PHƯƠNG TRÌNH.Dạng 1. Điều kiện xác định của phương trình.Dạng 2. Sử dụng điều kiện xác định của phương trình để tìm gghiệm của phương trình.Dạng 3. Phương trình tương đương, phương trình hệ quả.BÀI 2. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT VÀ PHƯƠNG TRÌNH BẬC HAI.Dạng 1. Phương trình tích.Dạng 2. Phương trình chứa ẩn trong giá trị tuyệt đối.Dạng 3. Phương trình chứa ẩn ở mẫu.Dạng 4. Phương trình chứa ẩn ở trong dấu căn.Dạng 5. Định lý Vi-et và ứng dụng.Dạng 6. Giải và biện luận phương trình.BÀI 3. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH BẬC NHẤT NHIỀU ẨN.Dạng 1. Giải và biện luận hệ phương trình bậc nhất hai ẩn.Dạng 2. Giải và biện luận hệ phương trình bậc nhất ba ẩn.Dạng 3. Giải và biện luận hệ phương trình bậc cao.Dạng 4. Các bài toán thực tế phương trình, hệ phương trình.

CHƯƠNG 4. BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH.BÀI 1. BẤT ĐẲNG THỨC.Dạng 1. Chứng minh bất đẳng thức dựa vào định nghĩa và tính chất.Dạng 2. Sử dụng bất đẳng thức Cauchy (Côsi) để chứng minh bất đẳng thức và tìm giá tri lớn nhất, nhỏ nhất.Dạng 3. Đặt ẩn phụ trong bất đẳng thức.Dạng 4. Sử dụng bất đẳng thức phụ.BÀI 2. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN.Dạng 1. Điều kiện xác định của bất phương trình.Dạng 2. Cặp bất phương trình tương đương.Dạng 3. Bất phương trình bậc nhất một ẩn.Dạng 4. Hệ bất phương trình bậc nhất một ẩn.BÀI 3. DẤU CỦA NHỊ THỨC BẬC NHẤT.Dạng 1. Xét dấu nhị thức bậc nhất.Dạng 2. Bất phương trình tích.Dạng 3. Bất phương trình chứa ẩn ở mẫu.Dạng 4. Bất phương trình chứa trị tuyệt đối.BÀI 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.Dạng 1. Bất phương trình bậc nhất hai ẩn.Dạng 2. Hệ bất phương trình bậc nhất hai ẩn.Dạng 3. Bài toán tối ưu.BÀI 5. DẤU CỦA TAM THỨC BẬC HAI.Dạng 1. Xét dấu của tam thức bậc hai áp dụng vào giải bất phương trình bậc hai đơn giản.Dạng 2. Ứng dụng về dấu của tam thức bậc hai để giải phương trình tích.Dạng 3. Ứng dụng về dấu của tam thức bậc hai để giải phương trình chứa ẩn ở mẫu.Dạng 4. Ứng dụng về dấu của tam thức bậc hai để tìm tập xác định của hàm số.Dạng 5. Tìm điều kiện của tham số để phương trình bậc hai vô nghiệm – có nghiệm – có hai nghiệm phân biệt.Dạng 6. Tìm điều kiện của tham số để phương trình bậc hai có nghiệm thỏa mãn điều kiện cho trước.Dạng 7. Tìm điều kiện của tham số để bất phương trình vô nghiệm – có nghiệm – nghiệm đúng.Dạng 8. Hệ bất phương trình bậc hai.

CHƯƠNG 5. THỐNG KÊ.BÀI 1. BẢNG PHÂN BỐ TẦN SỐ – TẦN SUẤT.BÀI 2. BIỂU ĐỒ.BÀI 3. SỐ TRUNG BÌNH – SỐ TRUNG VỊ – MỐT.BÀI 4. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN.

CHƯƠNG 6. CUNG VÀ GÓC LƯỢNG GIÁC, CÔNG THỨC LƯỢNG GIÁC.BÀI 1. CUNG VÀ GÓC LƯỢNG GIÁC.Dạng. Xác định các yếu tố liên quan đến cung và góc lượng giác.BÀI 2. GIÁ TRỊ LƯỢNG GIÁC MỘT CUNG.Dạng 1. Biểu diễn góc và cung lượng giác.Dạng 2. Xác định giá trị của biểu thức chứa góc đặc biệt, góc liên quan đặc biệt và dấu của giá trị lượng giác của góc lượng giác.Dạng 3. Chứng minh đẳng thức lượng giác, chứng minh biểu thức không phụ thuộc góc x, đơn giản biểu thức.Dạng 4. Tính giá trị của một biểu thức lượng giác khi biết một giá trị lượng giác.BÀI 3. CÔNG THỨC LƯỢNG GIÁC.

Xem thêm: Trang trọng kỷ niệm 50 năm chiến thắng “hà nội, 50 năm chiến thắng hà nội

Dạng 1. Tính giá trị lượng giác, biểu thức lượng giác.Dạng 2. Xác định giá trị của một biểu thức lượng giác có điều kiện.Dạng 3. Chứng minh đẳng thức, đơn giản biểu thức lượng giác và chứng minh biểu thức lượng giác không phụ thuộc vào biến.Dạng 4. Bất đẳng thức lượng giác và tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức lượng giác.Dạng 5. Chứng minh đẳng thức, bất đẳng thức trong tam giác.